I’m well aware of temperature stratification. It doesn’t happen in a microwave.
It empirically does. We can argue about the theory all day but the research says microwaves produce stratified temperature gradients when heating liquids. However, I’d point out that, in atmosphere, when we have localized hot spots the warm air can effectively travel in bubbles without significant mixing for quite some distance. There seems to be a similar phenomena at work when microwaving liquids.
See the screenshot below.
I pulled this from “Multiphysics analysis for unusual heat convection in microwave heating liquid” published in 2020 in AIP Advances.
Relevant excerpts:
“ Usually, the fluidity of liquids is considered to make the temperature field uniform, when it is heated, because of the heat convection, but there is something different when microwave heating. The temperature of the top is always the highest in the liquid when heated by microwaves.”
“ The experimental results show that when the modified glass cup with 7 cm metal coating is used to heat water in a microwave oven, the temperature difference between the upper and lower parts of the water is reduced from 7.8 °C to 0.5 °C.”
“According to the feedback from Midea (microwave appliance makers), when users use the microwave oven to heat liquids such as milk or water, the temperature at the top of the liquid will be significantly higher than the temperature at the bottom.”
That’s not really showing temperature stratification which is a more extreme separation of temperature from surface heating :
That’s just showing that the hottest atoms gather to the top, which btw, proves Convection currents.
Again, microwaves don’t heat purely the surface :
(a) Schematic diagram of convection in the bottom heated liquid and unusual convection in the microwave heated liquid and (b) schematic diagram of convection in liquids heated by microwaves with the modified glass.
The modified glass is just diverting the hotpots to the bottom to make the convection less “unusual”.
They aren’t claiming that convection doesn’t accrue, only that it’s “unusual convection” resulting in less even heating like that of thermal stratification, not literal thermal stratification where the layers have separate convection currents that prevent mixing all together.
That’s not really showing temperature stratification which is a more extreme separation of temperature from surface
I think the definition you are using is far too restrictive, in many contexts temperature stratification simply refers to a situation where you get temperature gradients across a fluid with the warmer fluid gathered near the top of the body. For example, in a factory you will often have “destratification” fans operating because warm air from equipment rising to the ceiling results in a temperature gradient from floor the ceiling.
It is not a phenomena exclusive to surface heating.
That’s just showing that the hottest atoms gather to the top, which btw, proves Convection currents.
Yes. My point was not to establish that convection is magically absent from fluids in microwaves, but to establish that it differs significantly from stovetop heating. Convection currents in stovetop heating create a strong stirring action that produces a substantially uniform temperature. Microwaves produce a significant nonuniform temperature gradient.
The modified glass is just diverting the hotpots to the bottom to make the convection less “unusual”.
Clearly. They make the heating more akin to a stovetop, which is really the point here.
They aren’t claiming that convection doesn’t accrue, only that it’s “unusual convection” resulting in less even heating like that of thermal stratification, not literal thermal stratification where the layers have separate convection currents that prevent mixing all together.
Once again, you are using a definition of thermal stratification that is far too specific. However, arguing over it is really just being pedantic because the core point at issue here is whether or not heating a cup in a microwave or a stovetop produce the same final product. They do not unless you apply some mechanical agitation to mix it up.
using a definition of thermal stratification that is far too specific
I’m using the textbook definition of which there are at-least three distinct layers that prevent mixing due to distinctly separate convection currents separated by the thermocline layer.
While the top has a considerable difference of ~18F at 95-113F, the rest is pretty evenly 77-86F.
By you’re less strict definition, after applying conventional bottom-up heating, Thermal stratification would also occur in this 2 layer form just by letting it sit and settle for a bit as the hotter atoms rise to the top due to their lower density creating a distinct hotter top with the rest holding a pretty even temp.
Matter of fact, the steam is just moister in the air combining with the hottest water atoms that are yeeting themselves out from the surface as vapor.
Search the literature for thermal stratification. There are many contexts where it is used outside of lakes and other large bodies of water, many of which do not consist of three distinct layers. Hell, the paper I cited SPECIFICALLY refers to the temperature gradient in the microwaved glass as “stratification”.
If you can’t understand the use of a term outside your specific area of expertise then thats honestly a you problem and that’s all I can say on that.
If the heating methods were as similar as you say, there wouldn’t be hundreds of publications accepted to various journals across the past two decades investigating the problem where microwaves produce a strong temperature gradient between the top and bottom of a body of liquid. It’s a well known process control problem.
I guess this does count as a more gradual example of thermal stratification where 35C is the thermocline layer.
However, by this definition, thermal stratification would still occur after applying conventional bottom-up heating by letting it sit and settle for some time allowing gravity to sort by density resulting in a very similar stable thermal stratification pattern.
You’d have to be constantly mixing or never take of the heat source to prevent this stable thermal stratification pattern from occurring.
I don’t think that is the case. A stratified fluid, in the absence of continued energy exchange with the outside environment, will eventually reach a homogenous temperature distribution due to diffusion.
That said, even if you are were correct, in the context of brewing tea we would only have a few minutes of brew time in which the stratification would have an impact on the extraction.
will eventually reach a homogenous temperature distribution due to diffusion.
Both would occur at the same time, infact much of the diffusion would be at the surface of the liquid because of the hotter atoms traveling up and it being an easier point of escape than going through the container.
in the context of brewing tea we would only have a few minutes of brew time in which the stratification would have an impact on the extraction.
Would stratification even matter in either case?
You still have to dunk the tea bag in, or pour the liquid, whichever way you do it. The only way I see this effecting tea extraction is if you microwave it with the tea bag included; and even then I’ve never noticed the difference.
It empirically does. We can argue about the theory all day but the research says microwaves produce stratified temperature gradients when heating liquids. However, I’d point out that, in atmosphere, when we have localized hot spots the warm air can effectively travel in bubbles without significant mixing for quite some distance. There seems to be a similar phenomena at work when microwaving liquids.
See the screenshot below.
I pulled this from “Multiphysics analysis for unusual heat convection in microwave heating liquid” published in 2020 in AIP Advances.
Relevant excerpts:
“ Usually, the fluidity of liquids is considered to make the temperature field uniform, when it is heated, because of the heat convection, but there is something different when microwave heating. The temperature of the top is always the highest in the liquid when heated by microwaves.”
“ The experimental results show that when the modified glass cup with 7 cm metal coating is used to heat water in a microwave oven, the temperature difference between the upper and lower parts of the water is reduced from 7.8 °C to 0.5 °C.”
“According to the feedback from Midea (microwave appliance makers), when users use the microwave oven to heat liquids such as milk or water, the temperature at the top of the liquid will be significantly higher than the temperature at the bottom.”
That’s not really showing temperature stratification which is a more extreme separation of temperature from surface heating :
That’s just showing that the hottest atoms gather to the top, which btw, proves Convection currents.
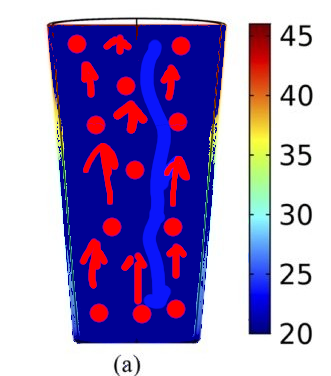
Again, microwaves don’t heat purely the surface :

The modified glass is just diverting the hotpots to the bottom to make the convection less “unusual”.
They aren’t claiming that convection doesn’t accrue, only that it’s “unusual convection” resulting in less even heating like that of thermal stratification, not literal thermal stratification where the layers have separate convection currents that prevent mixing all together.
I think the definition you are using is far too restrictive, in many contexts temperature stratification simply refers to a situation where you get temperature gradients across a fluid with the warmer fluid gathered near the top of the body. For example, in a factory you will often have “destratification” fans operating because warm air from equipment rising to the ceiling results in a temperature gradient from floor the ceiling.
It is not a phenomena exclusive to surface heating.
Yes. My point was not to establish that convection is magically absent from fluids in microwaves, but to establish that it differs significantly from stovetop heating. Convection currents in stovetop heating create a strong stirring action that produces a substantially uniform temperature. Microwaves produce a significant nonuniform temperature gradient.
Clearly. They make the heating more akin to a stovetop, which is really the point here.
Once again, you are using a definition of thermal stratification that is far too specific. However, arguing over it is really just being pedantic because the core point at issue here is whether or not heating a cup in a microwave or a stovetop produce the same final product. They do not unless you apply some mechanical agitation to mix it up.
I’m using the textbook definition of which there are at-least three distinct layers that prevent mixing due to distinctly separate convection currents separated by the thermocline layer.
While the top has a considerable difference of ~18F at 95-113F, the rest is pretty evenly 77-86F.
By you’re less strict definition, after applying conventional bottom-up heating, Thermal stratification would also occur in this 2 layer form just by letting it sit and settle for a bit as the hotter atoms rise to the top due to their lower density creating a distinct hotter top with the rest holding a pretty even temp.
Matter of fact, the steam is just moister in the air combining with the hottest water atoms that are yeeting themselves out from the surface as vapor.
Search the literature for thermal stratification. There are many contexts where it is used outside of lakes and other large bodies of water, many of which do not consist of three distinct layers. Hell, the paper I cited SPECIFICALLY refers to the temperature gradient in the microwaved glass as “stratification”.
If you can’t understand the use of a term outside your specific area of expertise then thats honestly a you problem and that’s all I can say on that.
If the heating methods were as similar as you say, there wouldn’t be hundreds of publications accepted to various journals across the past two decades investigating the problem where microwaves produce a strong temperature gradient between the top and bottom of a body of liquid. It’s a well known process control problem.
I guess this does count as a more gradual example of thermal stratification where 35C is the thermocline layer.
However, by this definition, thermal stratification would still occur after applying conventional bottom-up heating by letting it sit and settle for some time allowing gravity to sort by density resulting in a very similar stable thermal stratification pattern.
You’d have to be constantly mixing or never take of the heat source to prevent this stable thermal stratification pattern from occurring.
I don’t think that is the case. A stratified fluid, in the absence of continued energy exchange with the outside environment, will eventually reach a homogenous temperature distribution due to diffusion.
That said, even if you are were correct, in the context of brewing tea we would only have a few minutes of brew time in which the stratification would have an impact on the extraction.
Both would occur at the same time, infact much of the diffusion would be at the surface of the liquid because of the hotter atoms traveling up and it being an easier point of escape than going through the container.
Would stratification even matter in either case?
You still have to dunk the tea bag in, or pour the liquid, whichever way you do it. The only way I see this effecting tea extraction is if you microwave it with the tea bag included; and even then I’ve never noticed the difference.